Data: 30/09/2020
Título: On Undirected Two-commodity Integral Flow, Disjoint Paths and Strict Terminal Connection Problems
Palestrante: Alexsander A. de Melo, COPPE/UFRJ.
Data: 30 de Setembro de 2020, 16 h.
Sala: Google Meet.
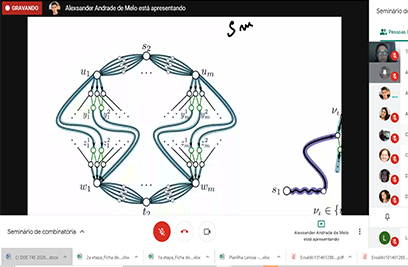
Resumo: Even, Itai and Shamir (1976) proved simple two-commodity integral flow is NP-complete both in the directed and undirected cases. In particular, the directed case was shown to be NP-complete even if one demand is unitary, which was improved by Fortune, Hopcroft and Wyllie (1980) who proved the problem is still NP-complete if both demands are unitary. The undirected case, on the other hand, was proved by Robertson and Seymour (1995) to be polynomial-time solvable if both demands are constant. Nevertheless, the complexity of the undirected case with exactly one constant demand has remained unknown. We close this forty year complexity gap, by showing the undirected case is NP-complete even if exactly one demand is unitary. As a by-product, we obtain the NP-completeness of determining whether a graph contains 1 + d pairwise vertex-disjoint paths, such that one path is between a given pair of vertices and d paths are between a second given pair of vertices. Additionally, we investigate the complexity of another related network design problem called Strict Terminal Connection.
Obs. This is a joint work with Celina M. H. de Figueiredo (PESC/COPPE/UFRJ) and Uéverton dos Santos Souza (IC/UFF).
Confira aqui a apresentação.





















 voltar
voltar