Data: 28/07/2021

Título: Results on the Graceful Game and Range-Relaxed Graceful Game.

Palestrante: Deise Lilian de Oliveira, IFRJ/UFF.

Data: 28 de Julho de 2021, 16 h.
Sala: Google Meet.

Resumo: The range-relaxed graceful game is a maker-breaker game played in a simple graph $G$ where two players, Alice and Bob, alternately assign an unused label $f(v) \in \{0,\ldots,k\}$, $k \geq |E(G)|$, to an unlabeled vertex $v \in V(G)$. If both ends of an edge $vw \in E(G)$ are already labeled, then the label of the edge is defined as $|f(v)-f(w)|$.

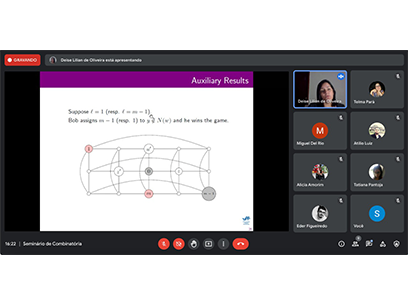
Alice’s goal is to end up with a vertex labelling of $G$ where all edges of $G$ have distinct labels, and Bob’s goal is to prevent this from happening.
When it is required that $k = |E(G)|$, the game is called graceful game. The range-relaxed graceful game and the graceful game were proposed by Tuza in $2017$.
The author also posed a question about the least number of consecutive non-negative integer labels necessary for Alice to win the game on an arbitrary simple graph $G$ and also asked if Alice can win the range-relaxed graceful game on $G$ with the set of labels $\{0,...,k+1\}$ once it is known that she can win with the set $\{0,...,k\}$.
In this work, we investigate the graceful game in Cartesian and corona products of graphs, and determine that Bob has a winning strategy in all investigated families independently of who starts the game.
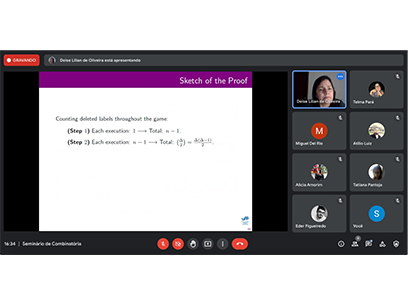
Additionally, we partially answer Tuza's questions presenting the first results in the range-relaxed graceful game and proving that Alice wins on any simple graph $G$ with order $n$, size $m$ and maximum degree $\Delta$, for any set of labels $\{0,\ldots,k\}$ with $k \geq (n-1) + 2\Delta\left(m-\Delta\right)+ \frac{\Delta\left(\Delta-1\right)}{2}$.

 Obs. This is a joint work with Atílio G. Luiz and Simone Dantas accepted in Eurocomb 2021.