Data: 26/10/2020
Título: On total coloring the direct product ir complete graphs.
Palestrante: Caroline Patrão, COPPE-UFRJ, IFG/IFRJ.
Data: 26 de outubro de 2020, 16 h.
Sala: Google Meet.
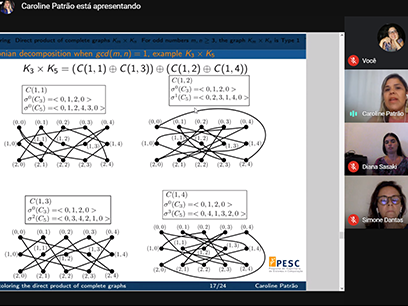
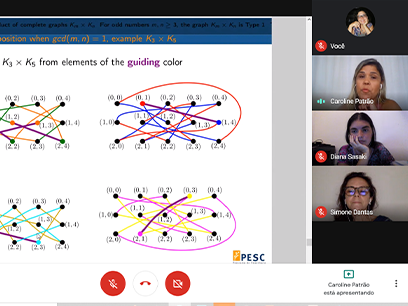
Resumo: A k-total coloring of a graph G is an assignment of k colors to the elements (vertices and edges) of G so that adjacent or incident elements have different colors. The total chromatic number is the smallest integer k for which G has a k-total coloring. The well known Total Coloring Conjecture states that the total chromatic number of a graph is either ∆(G) + 1 or ∆(G) + 2, where ∆(G) is the maximum degree of G. In this work, we consider the direct product of complete graphs Km×Kn. It is known that if at least one of integers m or n is even then, Km×Kn has total chromatic number equal to ∆(Km×Kn) + 1, except when m=n= 2. We prove that the graph Km×Kn has a total chromatic number equal to ∆(Km×Kn) + 1 when both m and n are odd integers, ensuring in this way that all graphs Km×Kn have total chromatic number equal to ∆(Km×Kn) + 1,except when m=n= 2.
Obs: This is a joint work with Celina M. H. de Figueiredo (COPPE-Universidade Federal do Rio de Janeiro), D. Sasaki (IME-Universidade Estadual do Rio de Janeiro), Luís Antonio Brasil Kowada (IC- Universidade Federal Fluminense), Diane Castonguay (INF-Universidade Federal de Goiás) and M. Valencia-Pabon (LIPN-Université Sorbonne Paris Nord).





















 voltar
voltar